Acesso direto aos capítulos
| AMEC | Opinião | Conselhos Corporativos | Em Pauta | Espaço Apimec |
| Fórum Abrasca | IBGC Comunica | IBRI Notícias | Mercado de Ações |
| Opinião | Orquestra Societária | Ponto de Vista | Sustentabilidade |
Espaço Apimec
TAXA DE RETORNO JUSTA: COMO CALCULAR O PRÊMIO POR RISCO DE MERCADO NO BRASIL por Antonio Zoratto Sanvicente e Mauricio R. A. Carvalho
O conteúdo discutido a seguir foi publicado recentemente, com maiores detalhes técnicos na Revista Brasileira de Finanças (ver Sanvicente e Carvalho, 2020). O tema básico desta discussão envolve a estimação do custo de oportunidade do capital, que possui diversas finalidades importantes.
Em si, o custo de oportunidade do capital é o retorno exigido justo por um investidor, levando em conta o risco percebido no investimento que está sendo analisado. Quando o mercado do ativo em questão está em equilíbrio, o retorno exigido é igual ao seu retorno esperado. Mas, ressalte-se, o que está sendo aqui discutido não é um procedimento para a previsão de retornos futuros.
Mesmo assim, o conhecimento do retorno exigido justo estimado é aplicável, para citar alguns exemplos importantes: (a) no cálculo de retornos esperados de ativos financeiros – feita a ressalva da condição de equilíbrio; (b) na fixação de taxas de retorno justas para concessões regulamentadas pelas agências do poder público, como nas áreas de rodovias, telecomunicações, energia elétrica, etc.; (c) na determinação de taxas de desconto para a avaliação de projetos de investimento; (d) no valuation de companhias em processo de fechamento de capital, ou seja, em ofertas públicas de aquisição (OPAs); (e) na fixação do custo de capital como benchmark de esquemas de remuneração variável de executivos, na linha do cálculo de valor criado para o acionista; (f) no cálculo de taxas de desconto exigidas em procedimentos de teste de asset impairment.
Na prática usual, os analistas recorrem à equação da chamada security market line, ou seja, ao CAPM, e um dos componentes fundamentais é o prêmio por risco da carteira de mercado (equity risk premium). Assim, o presente artigo discute uma metodologia que consideramos superior para a estimação do retorno esperado da carteira de mercado, do qual subtrai-se a taxa de juros livre de risco para a geração do prêmio por risco estimado.
Porque não usar o Prêmio por Risco Histórico
De maneira predominante, o retorno esperado da carteira de mercado, na prática, é estimado com base na média de retornos passados de um índice que se julga ser representativo do mercado, como o Ibovespa ou o S&P500. Desses retornos médios do índice é subtraída a média de retornos de um ativo tido como livre de risco (por exemplo, US Treasury Notes com prazo de 10 anos até o vencimento).
Para que tal enfoque tenha um mínimo de validade, pelo menos duas condições precisam ser satisfeitas: (a) a distribuição de probabilidades de retornos precisa ser “estável”, de modo a que um parâmetro, como a média, estimado com dados passados, seja representativo do que se espera ser a média no futuro; de maneira alternativa, seria dito que a “lei dos grandes números” é válida; (b) basicamente, que retornos passados podem ser extrapolados para o futuro.
No primeiro caso, as evidências são abundantes no sentido de que as distribuições de retornos variam substancialmente no tempo, especialmente quando as condições de mercado e da economia em geral se alteram. A alegação de que as séries históricas de um mercado desenvolvido, como o dos Estados Unidos, são mais longas, ou seja, que se dispõe de maior número de observações, não resolve o problema. E, a propósito, basta lembrar quantas mudanças importantes ocorreram no mercado norte-americano no período disponível (crise de 1929, Segunda Guerra Mundial, inflação de dois dígitos no início da década de 1980, crise financeira global em 2008, por exemplo).
No segundo caso, seria o mesmo que acreditar que o mercado não seria eficiente na forma fraca, ou seja, a versão menos exigente de todas; haveria a implicação de que bastaria observar retornos passados para prever retornos futuros, o que produziria uma regra simplória de investimento que todos nós gostaríamos de aplicar para ganhar dinheiro facilmente no mercado.
Uma das consequências graves do uso de médias de retornos históricos envolve o que fazer quando, no período escolhido, os retornos médios são negativos ou inferiores à taxa livre de risco, como ocorreu em 2008. Faria sentido dizer que o prêmio “justo” por risco seria negativo, ou seja, que o investidor deveria pagar para correr risco? (Este caso é ilustrado em Sanvicente, 2012, num estudo sobre a aplicação das Notas Técnicas da Agência Nacional de Transportes Terrestres – ANTT. No final de 2008, de acordo com o enfoque do prêmio histórico, o prêmio por risco seria de-6,60% ao ano – exatamente, um prêmio por risco negativo – ao passo que a metodologia que propomos estava indicando um prêmio de 14,22% ao ano.)
Cálculo do Prêmio Implícito – Base Teórica e Metodologia
Como acreditamos que o uso prêmio médio histórico não é apropriado, então que alternativa seria melhor utilizar? Propomos e utilizamos o cálculo do prêmio por risco implícito em cotações correntes de ações no mercado brasileiro, e o passo-a-passo do método empregado é exposto mais adiante.
Antes, porém, é bom salientar que usar dados correntes de mercado para a estimação de um valor implícito relevante não é inusitado. Basta lembrar dois casos: (a) o cálculo das taxas de inflação implícitas, obtidas pela diferença entre os juros futuros e as taxas de NTN-Bs, papéis indexados pelo IPCA; (b) a determinação de volatilidades implícitas em preços de mercado de opções, que serve de base para o índice VIX. Em particular, no segundo caso se pressupõe que um determinado modelo de precificação de opções é válido (Black-Scholes), e isso não causa desconforto para os usuários desse índice.
Além disso, o que propomos e utilizamos é praticado e divulgado por Aswath Damodaran, um professor de finanças nos Estados Unidos, muito seguido por analistas profissionais no mercado brasileiro. (Ver o seu site: http://pages.stern.nyu.edu/~adamodar/New_Home_Page/home.htm), sob o título Implied ERP, e atualizado mensalmente. Aswath Damodaran também discute as vantagens e desvantagens do uso de prêmios implícitos versus prêmios históricos em seu working paper: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3550293.
O ponto de partida em nossa metodologia de estimação é o chamado “modelo de Gordon”, originalmente proposto em Gordon (1959), que supõe que os dividendos de uma ação crescem a uma constante, g, por período. O valor intrínseco da ação corresponde ao valor presente da série de dividendos futuros, descontados à taxa ke, a saber, o custo de oportunidade do capital próprio da empresa. Dado que se supõe que os dividendos crescem a uma taxa constante, o valor intrínseco (V0) é o valor presente de uma série perpétua de fluxos de caixa, assim obtido:
![]()
Onde D1 é o dividendo por ação previsto para o final do primeiro período (ano).
Sob a hipótese de que os preços observados (P0) são iguais aos valores intrínsecos, a menos de um erro aleatório, podemos afirmar que os preços conterão informação sobre os retornos exigidos das ações, o que faz com retornos exigidos possam ser estimados da seguinte maneira, para cada ação individual:
![]()
A seguir, construímos o retorno exigido da carteira de mercado, o qual, como já explicado, se supõe ser igual ao seu retorno esperado, dada a equivalência suposta entre preços observados e valores intrínsecos, calculando a média dos retornos exigidos de uma amostra representativa de ações individuais. No trabalho publicado, utilizamos média simples, o que significa que a nossa proxy para a carteira de mercado é uma carteira equiponderada das ações nela contidas. Portanto, nossa igualdade suposta entre preços observados e valores intrínsecos não é considerada na base de ação por ação, mas na média para a amostra inteira que está representando o mercado.
Os preços P0 são diretamente observados. Dado que D1 = D0 (1+g), e D0 (dividendo corrente por ação) também é conhecido, a tarefa restante é estimar a chamada taxa de crescimento “sustentável” g (ver Ross et al., 2012). Ou seja, uma empresa poderá manter a taxa de crescimento de lucros e dividendos, sem alterar suas políticas de financiamento e dividendos, com base na seguinte relação:
![]()
onde ROE = return on equity, ou seja, lucro líquido depois do Imposto de Renda/patrimônio líquido, e b = taxa de retenção de lucros, ou (1 – payout).
Visto que informações sobre valores recentes de ROE, payouts e dividendos por ação estão disponíveis em demonstrações financeiras publicadas, e os preços são direta e continuamente observados, todos os dados necessários para a estimação de valores individuais de ke e o cálculo de sua média simples são dados facilmente acessíveis, e podem ser obtidos rapidamente numa base de dados como a da Economática.
Por sua vez, a taxa de juros livre de risco é obtida em cotações correntes de U.S. Treasury Notes. Visto que esses instrumentos pagam rendimentos em dólares norte-americanos, convertemos os dados do mercado local usando a taxa de câmbio entre Reais e dólares em cada data necessária.
A amostra de ações individuais é processada da seguinte maneira, a cada mês de análise:
- Coletam-se os preços de fechamento do mês, o lucro líquido por ação do período de 12 meses anteriores, os dividendos por ação dos 12 meses anteriores, e o valor patrimonial da ação. Ações não negociadas no final do mês são excluídas, o que deixa uma amostra de aproximadamente 90 ações, ou seja, um número superior ao dos componentes da carteira teórica do Ibovespa, o que é ainda mais importante quando se considera que ações de instituições financeiras não são incluídas na amostra, em vista das características especiais de suas demonstrações financeiras. Apenas a classe mais negociada de cada ação é utilizada. São excluídas as empresas cujos valores de lucro líquido e valor patrimonial da ação são negativos.
- Todos os valores são coletados em dólares da data da cotação para preços de mercado, da data da distribuição de dividendos, e da data do demonstrativo financeiro para lucro líquido e patrimônio líquido.
- ROE e payout são calculados: lucro líquido por ação/valor patrimonial da ação e dividendos por ação/lucro líquido por ação, respectivamente.
- ROE e payout são utilizados na estimação de g, conforme a equação (3). Empresas cujos payouts são superiores a 100%, resultando em valores negativos de g, são excluídas.
- A equação (2) é então utilizada na estimação de ke, dados os valores estimados de D1 e g e os preços P0 observados. São excluídos os valores extremos de ke, por meio de winsorização de 10% nas duas caudas da sua distribuição.
- É calculada a média simples dos valores individuais resultantes de ke. Essa é a estimativa do retorno exigido (esperado) da carteira de mercado.
- O último passo do cálculo do prêmio por risco da carteira de mercado consiste na subtração da taxa de juros livre de risco, com o yield to maturity corrente de U.S. Treasury Notes com prazo de 10 anos.
Aplicação do Cálculo de Prêmio Implícito no Mercado Brasileiro
O procedimento exposto na seção anterior resultou na seguinte série mensal do prêmio por risco implícito de mercado no Brasil, desde o final de janeiro de 1995 até o final de janeiro de 2021.
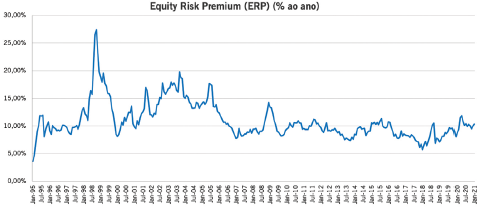
ERP Equity Risk Premium estimado = E(RM) - TBond 10 (% ao ano).
O cálculo para o qual se usa o procedimento descrito acima é mensalmente atualizado e divulgado gratuitamente na página do Centro de Estudos Quantitativos de Economia e Finanças (CEQEF) da Escola de Economia de São Paulo, Fundação Getulio Vargas. (Ver https://ceqef.fgv.br/bancos-de-dados). Ali podem ser encontrados os dados da série construída a partir de janeiro de 1995, e atualizada mensalmente, bem como documentação que explica o procedimento – acima reproduzido - adotado para a obtenção de prêmios anuais de risco para o mercado brasileiro.
Apresentamos a seguir uma planilha típica resultante desse procedimento. Neste caso, ela foi utilizada para a estimação do prêmio por risco no final de janeiro de 2021.
| Nome | P0 | LPA | VPA | DPA | ROE | PAYOUT | GROWTH | YIELD | K |
|---|---|---|---|---|---|---|---|---|---|
| Panatlantica | 7,1751 | 1,2248 | 5,3542 | 0,0347 | 0,2287 | 0,0283 | 0,2223 | 0,0059 | 0,2282 |
| Cyrela Realt | 4,6805 | 0,7601 | 2,8868 | 0,3559 | 0,2633 | 0,4682 | 0,1400 | 0,0867 | 0,2267 |
| Sao Martinho | 5,4402 | 0,4761 | 1,8708 | 0,1015 | 0,2545 | 0,2133 | 0,2002 | 0,0224 | 0,2226 |
| Sid Nacional | 5,5516 | 0,1425 | 0,6419 | 0,0016 | 0,2221 | 0,0110 | 0,2196 | 0,0003 | 0,2200 |
| Grazziotin | 6,4008 | 1,2160 | 5,6000 | 0,3317 | 0,2171 | 0,2728 | 0,1579 | 0,0600 | 0,2179 |
| Energisa | 8,9940 | 0,1629 | 0,6697 | 0,0245 | 0,2433 | 0,1506 | 0,2067 | 0,0033 | 0,2100 |
| Petrorio | 12,8728 | 0,6884 | 3,3340 | 0,0000 | 0,2065 | 0,0000 | 0,2065 | 0,0000 | 0,2065 |
| Portobello | 1,4536 | 0,1152 | 0,4813 | 0,0279 | 0,2393 | 0,2427 | 0,1812 | 0,0227 | 0,2039 |
| Celesc | 9,4962 | 1,6103 | 7,7777 | 0,4961 | 0,2070 | 0,3080 | 0,1433 | 0,0597 | 0,2030 |
| Cia Hering | 3,1520 | 0,3844 | 1,8058 | 0,0846 | 0,2129 | 0,2200 | 0,1660 | 0,0313 | 0,1973 |
| Lojas Renner | 7,5732 | 0,2807 | 1,1829 | 0,0619 | 0,2373 | 0,2206 | 0,1849 | 0,0097 | 0,1946 |
| JHSF Part | 1,3185 | 0,1868 | 0,9884 | 0,0264 | 0,1890 | 0,1413 | 0,1623 | 0,0233 | 0,1856 |
| Eletrobras | 5,0023 | 0,9583 | 8,5721 | 0,8560 | 0,1118 | 0,8932 | 0,0119 | 0,1732 | 0,1851 |
| Qualicorp | 5,6813 | 0,2458 | 1,1093 | 0,0541 | 0,2216 | 0,2202 | 0,1728 | 0,0112 | 0,1840 |
| Copel | 11,9213 | 2,1876 | 12,9938 | 0,5917 | 0,1684 | 0,2705 | 0,1228 | 0,0557 | 0,1785 |
| Metisa | 5,5297 | 0,9572 | 5,5695 | 0,1443 | 0,1719 | 0,1507 | 0,1460 | 0,0299 | 0,1759 |
| Engie Brasil | 7,8453 | 0,5180 | 1,5523 | 0,3285 | 0,3337 | 0,6342 | 0,1221 | 0,0470 | 0,1691 |
| BRF SA | 3,8752 | 0,2529 | 1,5555 | 0,0000 | 0,1626 | 0,0000 | 0,1626 | 0,0000 | 0,1626 |
| Smiles | 3,9208 | 0,4079 | 1,8745 | 0,2388 | 0,2176 | 0,5855 | 0,0902 | 0,0664 | 0,1566 |
| CPFL Energia | 5,6813 | 0,5416 | 2,2363 | 0,3471 | 0,2422 | 0,6408 | 0,0870 | 0,0664 | 0,1534 |
| Tran Paulist | 4,8120 | 0,6136 | 3,5870 | 0,3279 | 0,1711 | 0,5343 | 0,0797 | 0,0736 | 0,1532 |
| Celgpar | 12,9367 | 0,3819 | 2,5907 | 0,0000 | 0,1474 | 0,0000 | 0,1474 | 0,0000 | 0,1474 |
| Carrefour BR | 3,4771 | 0,2119 | 1,3199 | 0,0444 | 0,1605 | 0,2095 | 0,1269 | 0,0144 | 0,1413 |
| Ihpardini | 3,9427 | 0,1733 | 0,9808 | 0,0561 | 0,1767 | 0,3239 | 0,1195 | 0,0159 | 0,1354 |
| Rede Energia | 2,1458 | 0,0578 | 0,3258 | 0,0170 | 0,1774 | 0,2943 | 0,1252 | 0,0089 | 0,1341 |
| Aco Altona | 0,9003 | 0,1654 | 1,4143 | 0,0338 | 0,1169 | 0,2044 | 0,0930 | 0,0410 | 0,1340 |
| Padtec | 1,0373 | 0,0284 | 0,2155 | 0,0000 | 0,1318 | 0,0000 | 0,1318 | 0,0000 | 0,1318 |
| Energias BR | 3,5227 | 0,3832 | 2,9069 | 0,0899 | 0,1318 | 0,2346 | 0,1009 | 0,0281 | 0,1290 |
| Multiplan | 3,8715 | 0,2849 | 1,9044 | 0,0868 | 0,1496 | 0,3048 | 0,1040 | 0,0248 | 0,1288 |
| Brasilagro | 4,7079 | 0,4762 | 3,5985 | 0,1259 | 0,1323 | 0,2643 | 0,0974 | 0,0293 | 0,1267 |
| Tenda | 5,3087 | 0,3718 | 2,6619 | 0,0908 | 0,1397 | 0,2442 | 0,1056 | 0,0189 | 0,1245 |
| Baumer | 2,7356 | 0,2642 | 2,0682 | 0,0493 | 0,1278 | 0,1865 | 0,1039 | 0,0199 | 0,1238 |
| Trisul | 1,9723 | 0,1505 | 1,0922 | 0,0394 | 0,1378 | 0,2615 | 0,1017 | 0,0220 | 0,1237 |
| Ourofino S/A | 5,9789 | 0,2733 | 1,8138 | 0,0822 | 0,1507 | 0,3010 | 0,1053 | 0,0152 | 0,1205 |
| Tegma | 4,6111 | 0,2374 | 1,6668 | 0,0630 | 0,1424 | 0,2652 | 0,1047 | 0,0151 | 0,1197 |
| Kepler Weber | 6,7861 | 0,4583 | 3,4627 | 0,1006 | 0,1323 | 0,2196 | 0,1033 | 0,0164 | 0,1196 |
| Taesa | 5,8602 | 0,2764 | 0,9895 | 0,1951 | 0,2794 | 0,7057 | 0,0822 | 0,0360 | 0,1182 |
| M.Diasbranco | 5,5041 | 0,4293 | 3,4107 | 0,0884 | 0,1259 | 0,2058 | 0,1000 | 0,0177 | 0,1176 |
| Neoenergia | 3,2999 | 0,3551 | 3,0475 | 0,0842 | 0,1165 | 0,2371 | 0,0889 | 0,0278 | 0,1167 |
| Wlm Ind Com | 4,9745 | 0,2858 | 2,2320 | 0,0648 | 0,1281 | 0,2267 | 0,0990 | 0,0143 | 0,1133 |
| Enauta Part | 2,0910 | 0,2339 | 1,9824 | 0,2182 | 0,1180 | 0,9328 | 0,0079 | 0,1052 | 0,1131 |
| Vivara S.A. | 4,6531 | 0,1099 | 0,8375 | 0,0204 | 0,1312 | 0,1855 | 0,1068 | 0,0048 | 0,1117 |
| Cemig | 2,5019 | 0,2370 | 2,0199 | 0,1152 | 0,1173 | 0,4863 | 0,0603 | 0,0488 | 0,1091 |
| Localiza | 11,6657 | 0,2059 | 1,3509 | 0,0686 | 0,1524 | 0,3333 | 0,1016 | 0,0065 | 0,1081 |
| Eucatex | 1,2911 | 0,2431 | 2,7730 | 0,0416 | 0,0877 | 0,1710 | 0,0727 | 0,0345 | 0,1072 |
| SLC Agricola | 6,3241 | 0,3699 | 2,5721 | 0,1796 | 0,1438 | 0,4854 | 0,0740 | 0,0305 | 0,1045 |
| Schulz | 2,4471 | 0,1614 | 1,3508 | 0,0568 | 0,1195 | 0,3521 | 0,0774 | 0,0250 | 0,1024 |
| Weg | 15,3016 | 0,1774 | 0,9400 | 0,0890 | 0,1887 | 0,5014 | 0,0941 | 0,0064 | 0,1005 |
| Odontoprev | 2,5877 | 0,1168 | 0,4026 | 0,0927 | 0,2901 | 0,7933 | 0,0600 | 0,0380 | 0,0979 |
| Randon Part | 2,5402 | 0,1180 | 0,9365 | 0,0463 | 0,1260 | 0,3922 | 0,0766 | 0,0196 | 0,0962 |
| Eneva | 11,4319 | 0,3857 | 4,0866 | 0,0000 | 0,0944 | 0,0000 | 0,0944 | 0,0000 | 0,0944 |
| Irani | 1,0172 | 0,0558 | 0,5356 | 0,0125 | 0,1042 | 0,2240 | 0,0808 | 0,0133 | 0,0941 |
| Simpar | 6,4647 | 0,1653 | 1,5383 | 0,0322 | 0,1075 | 0,1948 | 0,0865 | 0,0054 | 0,0919 |
| Intermedica | 17,2574 | 0,2139 | 2,0678 | 0,0329 | 0,1034 | 0,1537 | 0,0875 | 0,0021 | 0,0896 |
| Hapvida | 3,1356 | 0,0430 | 0,3742 | 0,0109 | 0,1149 | 0,2542 | 0,0857 | 0,0038 | 0,0895 |
| Hypera | 5,8967 | 0,3423 | 2,6021 | 0,2193 | 0,1316 | 0,6407 | 0,0473 | 0,0390 | 0,0862 |
| Eztec | 6,6984 | 0,2915 | 3,1455 | 0,0528 | 0,0927 | 0,1812 | 0,0759 | 0,0085 | 0,0844 |
| Alupar | 4,6842 | 0,1208 | 1,1095 | 0,0408 | 0,1088 | 0,3380 | 0,0721 | 0,0093 | 0,0814 |
| Ger Paranap | 7,2865 | 0,4536 | 3,3265 | 0,3583 | 0,1364 | 0,7900 | 0,0286 | 0,0506 | 0,0792 |
| Ceb | 26,1144 | 1,0137 | 10,4384 | 0,3536 | 0,0971 | 0,3489 | 0,0632 | 0,0144 | 0,0776 |
| Itausa | 1,9376 | 0,1443 | 1,1486 | 0,1441 | 0,1256 | 0,9989 | 0,0001 | 0,0744 | 0,0745 |
| Unipar | 9,1309 | 0,3677 | 2,8672 | 0,2306 | 0,1283 | 0,6272 | 0,0478 | 0,0265 | 0,0743 |
| MRV | 3,4697 | 0,1910 | 2,0659 | 0,1001 | 0,0924 | 0,5243 | 0,0440 | 0,0301 | 0,0741 |
| Even | 2,0709 | 0,1140 | 1,5809 | 0,0262 | 0,0721 | 0,2301 | 0,0555 | 0,0134 | 0,0689 |
| BR Propert | 1,6436 | 0,1668 | 2,6336 | 0,0151 | 0,0633 | 0,0907 | 0,0576 | 0,0097 | 0,0673 |
| Grendene | 1,4080 | 0,0602 | 0,7218 | 0,0303 | 0,0834 | 0,5028 | 0,0415 | 0,0224 | 0,0639 |
| Tekno | 7,3413 | 0,5132 | 11,3080 | 0,3669 | 0,0454 | 0,7149 | 0,0129 | 0,0506 | 0,0636 |
| JBS | 4,4157 | 0,2005 | 2,6331 | 0,0971 | 0,0761 | 0,4842 | 0,0393 | 0,0228 | 0,0621 |
| Iguatemi | 6,2656 | 0,2324 | 3,1230 | 0,0870 | 0,0744 | 0,3742 | 0,0466 | 0,0145 | 0,0611 |
| Positivo Tec | 0,8273 | 0,0688 | 1,1759 | 0,0060 | 0,0585 | 0,0870 | 0,0534 | 0,0076 | 0,0610 |
| Alpargatas | 7,0929 | 0,0627 | 0,8827 | 0,0128 | 0,0710 | 0,2042 | 0,0565 | 0,0019 | 0,0584 |
| Duratex | 3,6286 | 0,1123 | 1,2531 | 0,0620 | 0,0896 | 0,5524 | 0,0401 | 0,0178 | 0,0579 |
| Cosan | 13,7073 | 0,4676 | 4,9101 | 0,2965 | 0,0952 | 0,6340 | 0,0349 | 0,0224 | 0,0572 |
| Jereissati | 4,4431 | 0,1894 | 3,2333 | 0,0213 | 0,0586 | 0,1123 | 0,0520 | 0,0050 | 0,0570 |
| Totvs | 5,1864 | 0,0784 | 0,8012 | 0,0401 | 0,0978 | 0,5113 | 0,0478 | 0,0081 | 0,0559 |
| Sao Carlos | 6,9614 | 0,2687 | 4,8605 | 0,0116 | 0,0553 | 0,0432 | 0,0529 | 0,0018 | 0,0547 |
| Cosan Log | 3,4369 | 0,0495 | 0,9596 | 0,0000 | 0,0515 | 0,0000 | 0,0515 | 0,0000 | 0,0515 |
| RaiaDrogasil | 4,5509 | 0,0439 | 0,4486 | 0,0247 | 0,0980 | 0,5611 | 0,0430 | 0,0057 | 0,0486 |
| Yduqs Part | 6,1268 | 0,1526 | 1,9548 | 0,0902 | 0,0781 | 0,5912 | 0,0319 | 0,0152 | 0,0471 |
| Log Com Prop | 6,1177 | 0,2530 | 5,3010 | 0,0370 | 0,0477 | 0,1463 | 0,0407 | 0,0063 | 0,0470 |
| Dimed | 3,9208 | 0,0718 | 1,1769 | 0,0257 | 0,0610 | 0,3582 | 0,0392 | 0,0068 | 0,0460 |
| Gerdau Met | 1,9321 | 0,0867 | 1,9024 | 0,0346 | 0,0456 | 0,3983 | 0,0274 | 0,0184 | 0,0458 |
| P.Acucar-Cbd | 13,7840 | 0,4231 | 8,6566 | 0,1072 | 0,0489 | 0,2535 | 0,0365 | 0,0081 | 0,0445 |
| Profarma | 1,1103 | 0,0636 | 1,4730 | 0,0000 | 0,0432 | 0,0000 | 0,0432 | 0,0000 | 0,0432 |
| Vale | 16,0613 | 0,5351 | 6,7265 | 0,4422 | 0,0795 | 0,8265 | 0,0138 | 0,0279 | 0,0417 |
| Gerdau | 4,2459 | 0,1478 | 3,2588 | 0,0613 | 0,0454 | 0,4149 | 0,0265 | 0,0148 | 0,0414 |
| Alianscsonae | 5,0421 | 0,1798 | 4,4063 | 0,0000 | 0,0408 | 0,0000 | 0,0408 | 0,0000 | 0,0408 |
| Metal Leve | 3,4497 | 0,1241 | 1,8483 | 0,1066 | 0,0671 | 0,8590 | 0,0095 | 0,0312 | 0,0407 |
| Média | 0,11429 |
Os títulos das colunas, além dos nomes das empresas que fizeram parte da amostra em janeiro de 2021 (observe-se que a amostra se altera a cada mês, especialmente em função da existência de cotações de suas ações), representam o seguinte:
P0 = preço mais recente da ação (classe mais negociada)
LPA = lucro líquido por ação nos 12 meses mais recentes divulgados
VPA = valor patrimonial da ação
DPA = dividendo por ação nos 12 meses mais recentes
ROE = LPA/VPA
Payout = DPA/LPA
Yield = DPA/P0
Growth = ROE x (1 – payout)
K = Yield + Growth
A tabela acima é usada para o cálculo do retorno esperado da carteira de mercado. Contém dados de 88 empresas, restantes após a aplicação dos filtros explicados anteriormente. Os retornos exigidos de cada uma das ações podem ser vistos na última coluna, em ordem decrescente, e a média resultante é igual a 11,43% ao ano. Note-se, em especial, que nenhum dos retornos exigidos é negativo. Com a subtração do yield to maturity de U.S. Treasury Notes de 10 anos, no valor de 1,08% em fins de janeiro de 2021, obtém-se o prêmio divulgado de 10,35% ao ano.
Uma simples análise visual do gráfico anteriormente apresentado chama a atenção para alguns pontos de alta da série: outubro de 1998 (crise da Rússia e contágio no Brasil, com a subsequente mudança de nossa política cambial), setembro de 2001 (atentados terroristas nos Estados Unidos), fevereiro de 2002 a setembro de 2003 (campanha presidencial que levou à eleição de Lula), e outubro de 2008 (quebra do Lehman Brothers e ápice da crise financeira global).
Tais momentos correspondem a períodos de crise nacional e/ou internacional, que provocaram quedas substanciais de cotações no mercado brasileiro de ações. E, de acordo com a nossa metodologia, isso equivale a aumentos do prêmio por risco. Afinal, se temos um aumento do nível de risco, o prêmio por risco sobe, e ele faz parte da taxa à qual são descontados os dividendos e lucros futuros esperados das ações, levando à queda de suas cotações. Como devia ser.
Análise dos Fatores Determinantes do Prêmio Implícito No Mercado Brasileiro
Num esforço de validação dos dados gerados pelo enfoque do prêmio implícito, realizamos análise de regressão para verificar que relação os prêmios assim calculados teriam com indicadores básicos do mercado de ativos com risco no Brasil.
O artigo considera nove indicadores facilmente observáveis, e conclui que quatro deles têm relação estatisticamente significante com a série de prêmios implícitos: (a) variações da taxa de juros de depósitos interfinanceiros (DI); (b) variações do prêmio por risco país (Brazil risk), (c) prêmio por liquidez (medido pela diferença entre taxas de juros de longo prazo e curto prazo de títulos públicos norte-americanos), (d) variações mensais do índice S&P500.
No caso dos três primeiros indicadores, o coeficiente obtido é positivo, representando o fato de que, quando o nível de risco aumenta, seus valores sobem, o que leva a uma elevação do prêmio por risco do mercado. No caso do quarto indicador (S&P500), o coeficiente é negativo: quando os preços de ações caem nos Estados Unidos, eles caem também no mercado brasileiro, o que corresponde a um aumento do prêmio por risco no mercado local. O valor do coeficiente de determinação ajustado por graus de liberdade (R2) dessa regressão é igual a 22,43%.
Em procedimento adicional de validação, construímos a série de prêmios históricos para o mesmo período analisado, e estimamos a mesma equação de regressão, com a qual o R2 ajustado foi de apenas 1,33%, não tendo obtido nenhuma relação significante com os mesmos indicadores de mercado considerados.
Resumo e Conclusões
Como foi destacado no texto deste artigo, o enfoque aqui proposto para a estimação do prêmio por risco de mercado apresenta algumas vantagens importantes: (a) é compatível com a lógica da análise financeira, no sentido de que não viola a hipótese de mercado eficiente na forma fraca, (b) acompanha os aumentos de níveis de risco com prêmios correspondentemente mais altos, (c) considera o que está ocorrendo no mercado no momento relevante, e utiliza informações contidas nos preços praticados, e em especial, (d) é um enfoque de aplicação fácil, em vista da ampla disponibilidade dos dados exigidos, e (e) já embute o risco Brasil na taxa, não se precisando fazer mais ajustes, exceto o de considerar os fluxos de caixa em dólares norte-americanos.
Julgamos, portanto, que este deveria ser o enfoque utilizado, nas várias aplicações práticas importantes que enumeramos no início do texto do artigo, para a determinação de valores de um parâmetro de avaliação tão relevante.
Bibliografia
Gordon, Myron J. (1959). Dividends, earnings and stock prices. Review of Economics and Statistics, 41(2), 99:105. Ross, Stephen A., Westerfield, Randolph J., Jaffe, Jeffrey. F. (2012). Corporate Finance, 11a ed. Boston, MA, McGraw-Hill. Sanvicente, Antonio Z. (2012). Problemas de estimação de custo de capital de empresas concessionárias no Brasil: uma aplicação à regulamentação de concessões rodoviárias. RAUSP, 47(1), 81:95. Sanvicente, Antonio Z., Carvalho, Mauricio R. A. (2020). Determinants of the implied equity risk premium in Brazil. Revista Brasileira de Finanças, 18(1), 69:90.
Antonio Zoratto Sanvicente
é professor titular - Escola de Economia de São Paulo, Fundação Getulio Vargas.
antonio.sanvicente@fgv.br
Mauricio R. A. Carvalho, CFA CNPI
é sócio-diretor da Condere Consultoria e Conselheiro Fiscal da Embraer e SLC Agrícola.
mauríciorac@insper.edu.br
Continua...


 Nº 297 • DEZ 25
Nº 297 • DEZ 25 Nº 296 • NOV 25
Nº 296 • NOV 25 Nº 295 • OUT 25
Nº 295 • OUT 25 Nº 294 • SET 25
Nº 294 • SET 25



